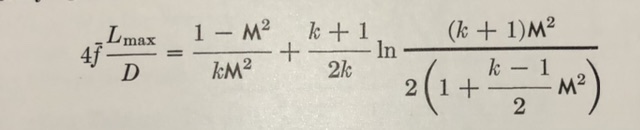Several Iterative Solutions within a Larger Iterative Solution

Engineering Software general discussion Spreadsheets
#1

Background
I plan to create a program to solve a compressible flow problem of an isentropic converging nozzle followed by an adiabatic pipe with friction:

Capture
Capture747Ă—162 10.7 KB

D is the diameter
k is the ratio of specific heats or isentropic coefficient for real gases
L is the length of the piping
M is the Mach number
MW is the molecular weight
N is the number of velocity heads lost in fittings
P is the absolute pressure
rho is the density
T is the temperature ( degrees C)
W is the mass flow rate
Z is the compressibility

Common inputs for all cases: N, L, g, Z, MW.

Common outputs for all cases: rho1, rho2, rho3, M1, M2, T2, P2.

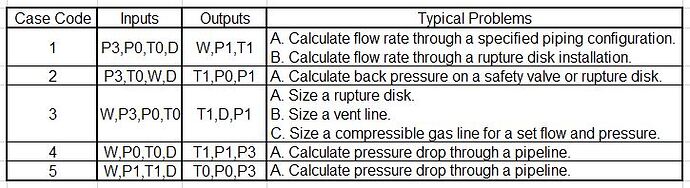
For Case 1 of 5, my inputs are P3, P0, T0, D. W, P1, T1 will be calculated.

Case 1 will simulate flow rate through a specified piping configuration, or flow rate through a rupture disk installation.

I think workflow will be like:
Estimate W explicitly.
Estimate M1 iteratively.
Estimate M2 iteratively
Calculate P2.
Is P2 = P3? If not, re-estimate W and repeat.

So, I’ve got two iterative calculations within one bigger iterative calculation.

Two options come to mind. Solve M1 and M2 every big iteration, or iterate M1 and M2 once every big iteration.

My program of choice is Excel. Can I do both ways without VBA? How? Which way is best? Or, should I be looking for a different program/language?

If at the end of the day, recall I have 4 more cases to go, I would like to have the security of the methodology locked down, does this affect the program/language I use?

Boredom and wanderlust have done me in again
#2

One way to do it would be to use the Solver to set P2 to P3, and estimate M1 and M2. The Solver has 3 different algorithms, if this is well behaved, and I think it will be, then the default should work.

Another option I have occasionally used is to go to File/options/formulas and tick the enable iterative calculations, and then use a circular reference to put some feedback into the algorithm.

To be honest I wouldn’t do any of that and would just go straight to Octave.

#3

are the equations in this ppt the ones you are using?
http://www.cchem.berkeley.edu/cbe150a/mom/CompressableFlow.ppt

#4

Yes and no. The isentropic nozzle equations are in there, but they chose to use isothermal pipe flow, not adiabatic pipe flow.

After completing my program, I was planning on extending what I did to include isothermal flow, or copy what I did and modify it to be a stand alone isothermal flow program, so this reference will be handy later. Thx!

I’m using The Dynamics and Thermodynamics of Compressible Fluid Flow by Ascher Shapiro in 1953.

#5

Yes, Solver came to my mind first too, but how to be sure the iterative calcs for M1 and M2 are converged, because Solver’s objective function can only be one cell. I was thinking of creating some residuals and residuals^2 using P2-P3 and M1i-M1i+1 and M2i-M2i+1 to drive them all to zero.

#6

Yup. In any machine learning you can only optimise one number. So I’ll assign a weighting to each response, and a target value, and some sort of error measure, often a quadratic. Then use solver to reduce the sum of (weighting*error) for all the numbers. If it comes up with the wrong answer, change weightings.

#7

Note that the form of the error function can be quite arbitrary. Sometimes I use a step function, but you can also do this in the Solver box, and insist that some values must be within certain constraints.

#8

I had not thought of a weighting factor, thanks.

Since I will be using Newton’s method on M1 and M2 to guide/accelerate each’s convergence, I can iterate each once, twice, thrice, or a dozen times for each Solver iteration. With cell math the number of iterations per pass will be hardwired. It could be variable in a more flexible programming language or environment.

#9

If you want to make this into a proper desktop application I can help with that.

#10

Can you explain that a bit more please? Not sure I know what that means or entails, but I am interested.

Is this something I need to plan for in the beginning, or can it wait until I have a working program and I want to document it, make it intuitive, etc.

Are you thinking of Excel or some other program?

#11

I can code in several different languages. If you want it either singularly or with several other things so it’s like an engineers toolbox, I can do that.

#12

Are you sure this is iterative?
To clarify my question, are you looking for the steady-state flow from this discharge, or the transient flow as the discharge is initiated until it reaches a steady condition?
Does your problem have a limited or infinite volume at points “0” and “3”?

Discharge is generally treated (in my context) as a deterministic problem that can be solved directly, provided you can fix enough of the conditions to known values. Sometimes you just pick a discharge coefficient and get on with it.

For a long pipe with friction, then I agree that there’s a lot going on that would determine the discharge coefficient. Sweeping it away with one value would reduce the effort but probably the usefulness of your analysis, since it seems like the friction in the pipe is the key point of interest. That said, if the method to solve for a simple orifice is not an iterative problem, then I wonder why you have assumed that a pipe with friction should be.

Are you solving for subcritical flow, choked flow, or both? Another simplification is possible if you only have one case to deal with.

#13

The reservoir (0) / pressure vessel and receiver (3) / atmosphere are assumed infinite. It is a steady-state flow analysis. Here’s one of the equations to be solved for Mach number:

image

My methodology will solve for subcritical flow and critical flow, whichever it is per the input.

I’m working on Case 1. There are 4 more after this:

Capture
Capture725Ă—198 47.7 KB

#14

Yeah that doesn’t look as if you can solve for M analytically. I can’t get Wolfram Alpha to help either.

#15

I’m pretty sure it can be differentiated and iterated to an acceptable solution using Newton’s method. If not analytically, for sure numerically.

#16

Sorry, I meant reorganise the equation to give M^2=…

Anyway, for f=0.1,L=10,D=0.1, k=1.4 I get M=0.1271, and the plot of error vs Mestimate is continuous and always increasing in the range 0<M<1

#17

With a ln? Not sure you can get just an M^2 on the LHS.

I believe it is a well behaved function.

#18

FYI, I haven’t coded a thing yet. Just working with pencil and paper and researching now to get as efficient a solution (flow charting) as I can before coding.

It won’t be long though.

Also, I’m only working on it on the weekends. Too much real work to do M-F!

#19

I’m a bit surprised non VBA Excel doesn’t have the equivalent of fsolve, which solves f(x)=0 . So yes I don’t hold out any great hope for a single line solution for M.

#20

A plot of M vs fL/D for a given k says you could probably fit a single line function to it, if my sums are right

1 Like