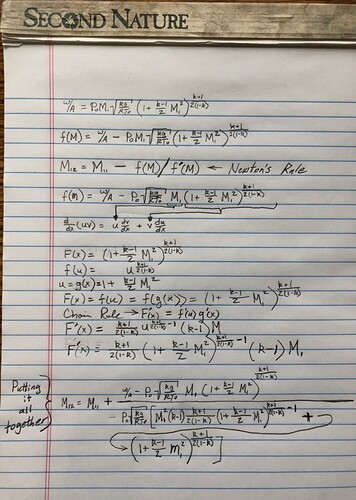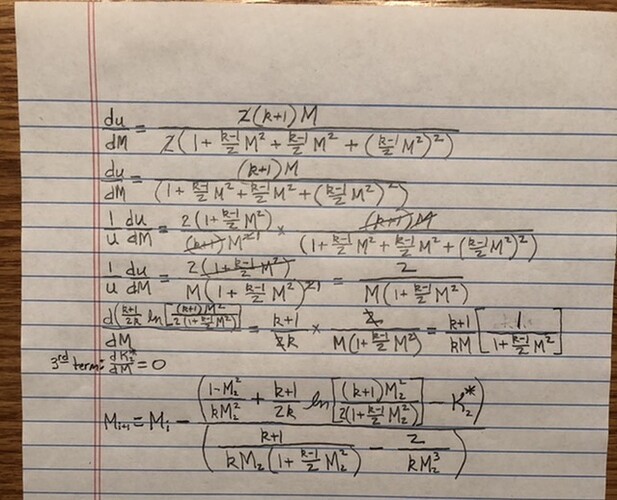I’m pretty sure it can be differentiated and iterated to an acceptable solution using Newton’s method. If not analytically, for sure numerically.
Sorry, I meant reorganise the equation to give M^2=…
Anyway, for f=0.1,L=10,D=0.1, k=1.4 I get M=0.1271, and the plot of error vs Mestimate is continuous and always increasing in the range 0<M<1
With a ln? Not sure you can get just an M^2 on the LHS.
I believe it is a well behaved function.
FYI, I haven’t coded a thing yet. Just working with pencil and paper and researching now to get as efficient a solution (flow charting) as I can before coding.
It won’t be long though.
Also, I’m only working on it on the weekends. Too much real work to do M-F!
I’m a bit surprised non VBA Excel doesn’t have the equivalent of fsolve, which solves f(x)=0 . So yes I don’t hold out any great hope for a single line solution for M.
A plot of M vs fL/D for a given k says you could probably fit a single line function to it, if my sums are right
For k=1.4
M=.7388(4fL/D)^-0.477
Yes, that’s great for an initial guess. Thank you. The equation you curve fit is only for the pipe. I still want to converge on the solution of the isentropic reservoir attached to the pipe. I think there are 2 (or 3?) equations that need simultaneous iterative solutions since the same w goes through the isentropic nozzle and pipe. Initially several variables are assumed, like viscosity and f, and later calculated as the T and P profile unfold.
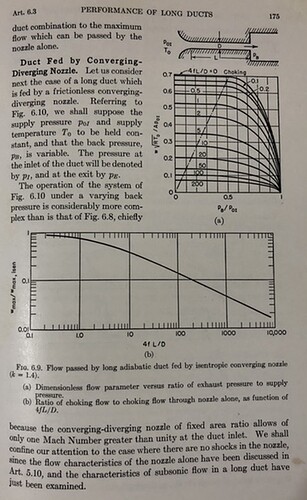
In fact, I have similar in my hand calcs already, see Fig 6.9 (b):
My initial guess on w and M1 are coming from just the isentropic reservoir.
I will keep this in mind as I progress. It may be handy in a different Case if I do not have To and/or Po, like Case 2 and 5 (see previous post). Many thanks!
So by doing a curve fit for each of the sub tasks you can reduce it to one loop, which Solver will be quite happy with.
Yes, I will be looking into that.
I’m no mathematician, so if this bears no validity to the discussion one of the moderators can delete it, but . . .
Years ago I was part of developing a qick-calculating method to determine the optimal way to distribute / apportion the available flow of a river between sixteen generating units divided into four different classes of flow curve.
The initial way this was to be performed consisted of an iterative process within an iterative process, which I was told yielded a calculation time [ reportedly in tens of minutes, IIRC ] far too slow to be satisfactory for the application.
A remedy was found when some math guru from Queen’s University in Kingston, Ontario [ Canada ] came up with some formula using quadrential calculus [ sp? ] that did the calculation in one second or so.
Useful info?
It sounds interesting, but I won’t know until I Google it and see what I can learn. Thanks for the lead.
I had a bit of free time, so I worked on the solution of M1 at the exit of the isentropic nozzle:
I programmed this bit into Excel and gave it 5 iterations. As long as my guess is between -3 < M < 3 it converges to 16 digits accuracy to a value of about M = 0.083.
Admittedly, this has been a 2 martini problem! That is NOT my first, or second, sheet of paper!
Been a while since I looked at anything like this, so flame me if you wish…
If “L” is sufficiently long, P3 is irrelevant. If “L” is sufficiently short, it’s just a venturi exercise. ??
Correct!
If “L” is sufficiently long, it is frictionally choked.
I’d say your on the right track with Newton’s method. It may or may not be helpful but I utilized the method for a 4 variable problem a bit ago and have an excel sheet on github I could point you to.
To make those hand calcs slightly easier give Maxima a try it’s an open source computer algebra system (CAS) program worked wonders for me on some very symbolic double integrals I needed to do, https://maxima.sourceforge.io/
Maxima looks very interesting! My company maintains a vise-like grip on our laptop’s security. It’s a blessing, no hacks ever, and a curse, I have no administrative control at all. So, I’m struggling if it will be worth the effort, plus, I’m old school. I’ve been doing hand calcs for decades! @Celt83, could you start a thread on Maxima under Engineering Software and explain/highlight just a few things you really like about it! Any pictures/screenshots worth a thousand words, type thing? That’ll give me some real application to consider if I want to approach the IT police, as we call them.
I took last weekend off from this problem, but this weekend I was able to get through the derivation of the solution to M2:
And I was able to program it into the Case 1 spreadsheet and get a converged solution to the example I’m testing.
Next weekend I’ll attempt to tie the isentropic nozzle (M1) and pipe (M2) solutions together using Solver to converge on M2 = 1 and/or P2 = P3. I think that may be the trickiest part!
I refreshed my recollection on Solver this morning. It looks straightforward to set the objective function to P3 - P2 = 0 with a constraint that M2 <= 1 and adjust the mass flow rate, W.
What could possibly go wrong? 
We’ll see next weekend. Back to the work that pays the bills.