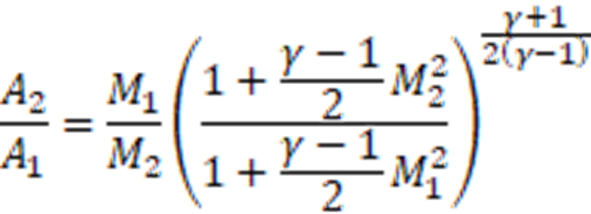A Simple Numerical Method for Gas/Vapor Flow in a Safety Valve

Chemical Engineering general discussion Safety Relief Valve (PSV)
, ,
#1

One of the ways I have learned a technology is to get down into the basics and derive key working equations that are found in the references.

It is common practice to model a safety valve on a pressure vessel as a flow nozzle, and NOT as an orifice. The theoretical model from the pressure vessel to the throat of the flow nozzle is an isentropic converging flow nozzle:

"* * * *

       *
        *
         *
           ******

Flow [→] ----- - ----- Z = 0, adiabatic, frictionless

           ******
         *
        *
       *

'* * * *
[^]--------------------[^]---------------------[^]
Po,Go ------------- Pn.Gn -------------- Pback pressure

Derivation
P/ρ + V2/2gc + gZ/gc = constant Bernoulli’s equation
Z = 0
P/ρ + V2/2gc = constant

Differentiate
dP/ρ + d [ V2/2gc ] = 0
G = w/A = ρV Continuity equation
V = G/ρ and, therefore, V2 = (G/ρ)2

Substitute and rearrange
d [ (G/ρ)2 /2gc] = - dP/ρ

Integrate
∫ d [ (G/ρ) 2 /2gc ] = - ∫ dP/ρ Equation 1

Integrate LHS of Equation 1 from Go to Gn
[(Gn/ρn)2 - (Go/ρo)2] /2gc = - ∫ dP/ρ
Go ≈ 0 because Ao is usually very large compared to An
(Gn/ρn)2 = - 2gc ∫ dP/ρ
(Gn/ρn) = ( - 2gc ∫ dP/ρ )1/2
Gn = ρn ( - 2gc ∫ dP/ρ )1/2

Evaluate ∫ dP/ρ (the RHS of Equation 1) numerically from Po to Pn until Gn reaches a maximum (sonic flow) OR Pn = Pbp (subsonic flow).

The beauty of this method is . . . . no restrictive assumptions were made!

Notes

  1. The method was derived with the nozzle oriented horizontally. Most safety valve nozzles are oriented vertically. However, gas pressure changes very little with elevation changes due to the small density of a gas. It is common practice to ignore this effect on gas flow evaluations. This is especially true for the small elevation change from the pressure vessel to the safety valve nozzle on most safety valve installations.
  2. We did not assume an ideal gas. Any PVT relationship can be used to calculate the temperature and density at each pressure increment in the numerical integration.
  3. Pressure increments should be chosen sufficiently small for accuracy and sufficiently large for calculation speed. A dP = 1% of the safety valve set pressure is a good starting point. For most problems, a dP = 1 psi works quite well.
  4. The method is extremely easy to implement in a spreadsheet. I created a spreadsheet which uses the ideal gas law as the PVT relationship. A copy of the input and output is included further below.

Nomenclature
P = pressure, lbf/ft2
ρ = density, lbm/ft3
V = velocity, ft/sec
g = gravitational acceleration, 32.174 ft/sec2
gc = gravitational constant, 32.174 lbm.ft/lbf/sec2
Z = elevation, ft
G = mass velocity, lbm/ft2/sec
w = mass flow rate, lbm/sec
A = area, ft2

Subscripts
o = in the vessels straight side and head space.
n = in the throat of the nozzle.
back pressure = the pressure of the surroundings where the gas exits the nozzle. In a safety valve, this is the back pressure created by the tailpipe attached to the outlet connection.

Copy of Isentropic Nozzle.xls:

Po = 100 psia dP = 1 psia
To = 25 C
MW = 29 lb/lb.mole
k = 1.4
dnozzle = 1 inch

Pn = 53 psia
Tn = -24.5 C
ρn = 0.320 lbm/ft3
Σ(dP/ρave) = -115.293 lbf.ft3/(in2.lbm)
Gn = 330.746779 lbm/(ft2.sec)
w = 6494 lbm/hr

Pn Tn ρn Σ(dP/ρave) G w
psia oC lbm/ft3 lbf.ft3/(in2.lbm) lbm/(ft2.sec) lbm/hr
100 25.0 0.504
99 24.1 0.500 -1.993 67.944540 1334
98 23.3 0.496 -4.000 95.566345 1876
97 22.4 0.493 -6.022 116.401889 2286
96 21.5 0.489 -8.059 133.663328 2624
95 20.7 0.485 -10.111 148.601443 2918
94 19.8 0.482 -12.178 161.860800 3178
93 18.9 0.478 -14.262 173.826018 3413
92 18.0 0.474 -16.361 184.748745 3628
91 17.1 0.471 -18.477 194.804455 3825
90 16.2 0.467 -20.609 204.121365 4008
89 15.2 0.463 -22.759 212.796582 4178
88 14.3 0.460 -24.926 220.905767 4337
87 13.4 0.456 -27.110 228.509242 4487
86 12.4 0.452 -29.312 235.656017 4627
85 11.5 0.448 -31.533 242.386553 4759
84 10.5 0.445 -33.773 248.734707 4884
83 9.5 0.441 -36.031 254.729138 5002
82 8.6 0.437 -38.310 260.394347 5113
81 7.6 0.433 -40.608 265.751468 5218
80 6.6 0.429 -42.926 270.818868 5318
79 5.6 0.426 -45.265 275.612616 5412
78 4.6 0.422 -47.626 280.146852 5501
77 3.5 0.418 -50.008 284.434085 5585
76 2.5 0.414 -52.412 288.485432 5664
75 1.5 0.410 -54.840 292.310811 5740
74 0.4 0.406 -57.290 295.919101 5810
73 -0.6 0.402 -59.764 299.318276 5877
72 -1.7 0.398 -62.263 302.515514 5940
71 -2.8 0.394 -64.786 305.517290 5999
70 -3.9 0.390 -67.335 308.329458 6054
69 -5.0 0.386 -69.910 310.957313 6106
68 -6.1 0.382 -72.512 313.405650 6154
67 -7.2 0.378 -75.141 315.678815 6198
66 -8.4 0.374 -77.798 317.780744 6240
65 -9.5 0.370 -80.485 319.715001 6278
64 -10.7 0.366 -83.201 321.484810 6312
63 -11.9 0.362 -85.947 323.093080 6344
62 -13.1 0.358 -88.725 324.542432 6372
61 -14.3 0.354 -91.535 325.835216 6398
60 -15.5 0.350 -94.378 326.973534 6420
59 -16.7 0.345 -97.256 327.959251 6439
58 -18.0 0.341 -100.168 328.794009 6456
57 -19.2 0.337 -103.116 329.479243 6469
56 -20.5 0.333 -106.102 330.016186 6480
55 -21.8 0.329 -109.126 330.405881 6488
54 -23.1 0.324 -112.189 330.649185 6492
53 -24.5 0.320 -115.293 330.746779 6494
52 -25.8 0.316 -118.439 330.699170 6493
2 Likes
#2

@pxyarala It took me a while to find my old spreadsheet. I haven’t touched it in about 7 years, so my recollection of the details in it may be a bit hazy. I did fix a small bug in it before I uploaded it. Here it is for your use:

Isentropic Nozzle.xls (254 KB)

#3

Thanks Latexman. Your spreadsheet clears all my questions actually!!!. I will complete my work and post my results to you.

Thanks and Regards,
Pavan Kumar

#5

I am doing the PSV Sizing for Two Phase flashing flow service using HEM Direct Integration Method in API 520 Part 1 C 2.1.1.3. The method uses the calculation of the mass flux using the integral which is same as the one you have in your spreadsheet. I was running into some issues with my calculations and upon looking at your spreadsheet I seem to have understood the mistake. I will complete my calculations and post my results in my next message hopefully by today evening. I also need to calculate the PSV outlet line pressure drop. I have tried using the API 521 5.5.10 method and ran into problems. I shall post those calculations also. Would you be able to help me there too?.

Thanks and Regards,
Pavan Kumar

#6

Pavan, I’ll do my best to help you, but I don’t think I’ve ever done the two phase integrel method. For the two phase methodology and two phase outlet line pressure drop could you start new topics please? My topic/FAQ is about vapor only flow, so it’s different enough for a new thread. But, no matter how you post them, I’ll reply.

#7

@Latexman , thank you very much for providing the tool. I’m working with saturated steam and my goal is to calculate the built-up back pressure of a given system. My calculation using this worksheet ends up at (Pn,Tn), which is below the saturated vapor line. There are some papers (e.g. doi.org/10.13140/RG.2.2.11861.29927 ) which provide some equations for convergent nozzle, etc. On the other hand, some PSV suppliers provide so-called “Capacity saturated steam (incl. 10% overpressure)” in kg/hr as a function of steam set pressure and the valce characteristics. My question is whether I can somehow use this number to assess Pn,Tn? Thanks for the help. Regards,Alex

#8

@Al6o My spreadsheet is pretty simplistic. I used it many years ago to understand basic PSV sizing methodology. I use more sophisticated tools to size PSVs for purchase, like company supplied tools, Aspen+, or PSV vendor tools. These tools consider real gas/vapors behavior, the flow of real nozzles, and other factors.

My spreadsheet assumes the flow nozzle is perfect (coefficient of discharge = 1) and the gas/vapor is an ideal gas (Z = 1), which means it’s not even looking for a saturation line or nonidealities. As I said, it’s pretty simple.

Can you use a vendor’s capacity data to assess Pn, Tn? IMO, not directly. The vendor’s capacity data I’ve seen does not tell you Pn, Tn. They tell you capacity (kg/hr). If you obtain the certified flow coefficient of the PSV you are modelling, AND knowing that these flow coefficients are already discounted by some safety factor by the certification agency, I think you can compare it indirectly by comparing flows (w). Note - here in U.S. the flow coefficient is discounted 10% by the ASME and the National Board of Boiler and Pressure Vessel Inspectors, so the actual flow is 10% higher.

Then, in my spreadsheet by choosing a MW that includes compressibility effects (Z) and a k for the real fluid, you could compare the calculated flow (w) to the vendor’s capacity. They should differ by the certified flow coefficient corrected by the agencies safety factor.

I speak in generalities because I do not know EU PSV agency practice.

@pxyarala do you have any input for Alex? You downloaded my spreadsheet about 2 years ago, and we talked about it and other things then off-line.

#9

@Latexman Thanks a lot for the clarification. That is very useful. If you don’t mind, I keep asking you some trivial questions.

#10

@Al6o Okay, I’ll try my best to answer them.

#11

@Latexman Following your comments, I have introduced the index of isentropic expansion (n=1.135 for dry saturated steam). In addition, rho_0 is now taken from the steam table. Looks it may be good enough to be a first approximation (TBC).
Having Pn,Tn and dm/dt_n I can assess the pressure drop over my pipeline. Now I am struggling with conclusions. Do I understand correctly that if the built-up back pressure is above 10% of the set pressure a given design is not acceptable? Thanks for your guidance.

#12

For a conventional PSV, 10% backpressure is usually excessive and it affects it’s performance too much. If reducing the backpressure is too expensive, consider changing to a balanced bellows PSV; it can usually handle up to 30% backpressure relative to set pressure. Beyond 30% backpressure, look at pilot-operated PSVs. The % overpressure they are good for depends on type used; consult manufacturer’s and/or their catalog.

#13

@Latexman I’m currently attempting to go one step further and simulate my system, which consists of a PSV valve and a long discharge pipe that terminates in a caisson(release to atmosphere). Saturated steam is the fluid. The aim is to assess a maximum pressure the discharge pipe (to set a pressure rating). On the other hand, the simulation helps to validate my considerations.It appears from your posts that you have been using a specialized software for this. Could you please tell me which one? Thanks a lot.

#14

The software I use was written by my company’s fluid flow technology center. One software sizes the PSV and evaluates a single diameter inlet and a single diameter outlet. If multiple diameter inlet or outlet is needed, I have another software. They are not commercially available. It’s considered proprietary technology, but it’s about 20 years old.

I know Aspen+ can do this, I’ve used that too. HYSYS probably does it too, idk for sure.

The outlet pipe and fittings are usually assumed to be adiabatic, compressible flow. A good reference to start with is:
Solving Adiabatic Compressible Flow.pdf (122.4 KB)

I’m sure there’s lots of other commercially available software out there that can be used.

#15

Thanks a lot! I will try Aspen PLUS.

#16

@Latexman I apologize for troubling you once more with this matter. There are two pipe segments with different sizes in my discharge line. Is the area-Mach number relation applicable in this case?
image
which was derived for isoenergetic-isentropic flow. Should it be adiabatic expansion?
How can I assess (P2,T2,Ma2) at the entrance of the second pipe?
Thanks!

#17

Sorry, with the company tools I have, I’ve never had to figure that out. I’ll have to noodle on it.

I did replace the link in my post above with the .pdf. That doesn’t have the answer to your question, but it is more convenient than the link.

#18

Your problem is related to saturated steam, but most models I know of use diatomic gases.
How similar are they? Probably not.
If you want to explore the “perfect” gas models I can point you to some references.

Maybe an “exact” answer for a diatomic gas can be adjusted for steam or saturated steam?

#19

Try looking at this and let me know if you think it’s relevant enough.

SmithC_CalculationofFlowofAir.pdf (1.2 MB)

There’s more where that came from.

#20

The NUSC Technical Report 6150 is probably more complex than your PSV outlet pipes but it does give a lot of detail, methodology, and references that could come in handy developing a solution.

#21

@Latexman @SparWeb Thanks a lot for the references. I will dig into details and post my results