For as long as I’ve been building wind turbines, I’ve been using permanent magnets in the generator to fabricate a rotor that is self-exciting. It drastically simplifies the electrical system by doing away with circuits to energize a field and also allows for a direct-drive between rotor blades and the generator.
I’ve recently taken an interest in the possibility to use an induction motor instead. This requires me to figure out some difficult things, because I do NOT want to use a gearbox to mate the rotor blades, which only operate in the 100-500 RPM range. I’m trying to find my way to an induction motor that will self-excite in this speed range, and yet not need 16 or 20 poles.
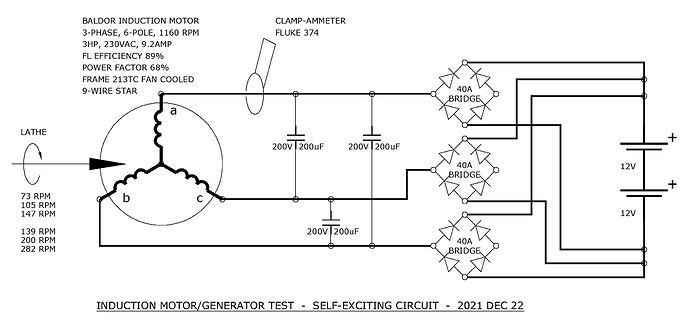
At this point, I’m still reading and doing the math so that I can understand what’s possible, reasonable, and what’s impossible. If any possibilities open, I have some stock 3-phase motors that I can do some experiments with. I also have a lathe, which can be used to drive the motor’s shaft at variable speeds to simulate operation as a generator.
I’m also keenly aware that “this has been tried before”, and by people who know much more (and much less) than me. So I humbly explore the art of the possible.
If starting with a common 4-pole 3-phase induction motor, its synchronous speed will be 1800 RPM but with slip it will normally run at about 1700 RPM. As a generator, slip reverses, so you would expect about 1900 RPM where the now-generator can produce about as much power as it could consume when it was a motor. Since the VARs are always a waste, that’s not perfectly true.
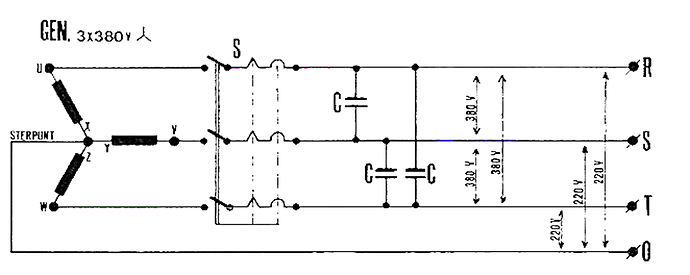
To make it generate, it can be excited by a bank of capacitors. The capacitors apply a magnetizing current that will grow large enough at the synchronous speed to stabilize the gap flux so that real power can be generated. The capacitors have to be sized correctly for this to work. The math for this is relatively straightforward, but I haven’t been finding it in common textbooks about motors. I will post some examples of tech journal papers that I have found that have informed me of the capacitor sizing math. For a common industrial 3-HP motor I expect the three capacitors to be rated about 200 uF and 300V, which is common enough though not cheap.
This is where I think my curiosity gets me into trouble. I want this induction motor to self-excite at a speed MUCH lower than 1900 RPM. More like 1/10 of that, i.e. < 200 RPM. If this is possible, this would allow direct drive of the rotor to the induction generator with no gearbox.
But so far I’m coming up with math that goes out of whack. To self-excite at lower speed (hence, lower frequency) the value of the capacitor needs to increase substantially. Using the speed ratio that I suggested above, the synchronous frequency of the generator is only 6 Hz, not 60 Hz.
That drives a capacitor value of 10^2 greater than it was before, or 20 milliFarads, still at 300V. I think the math is right, but that seems like unobtainium, to me.
Can anyone relate to this line of thinking? Any insight into how close my math is to reality?